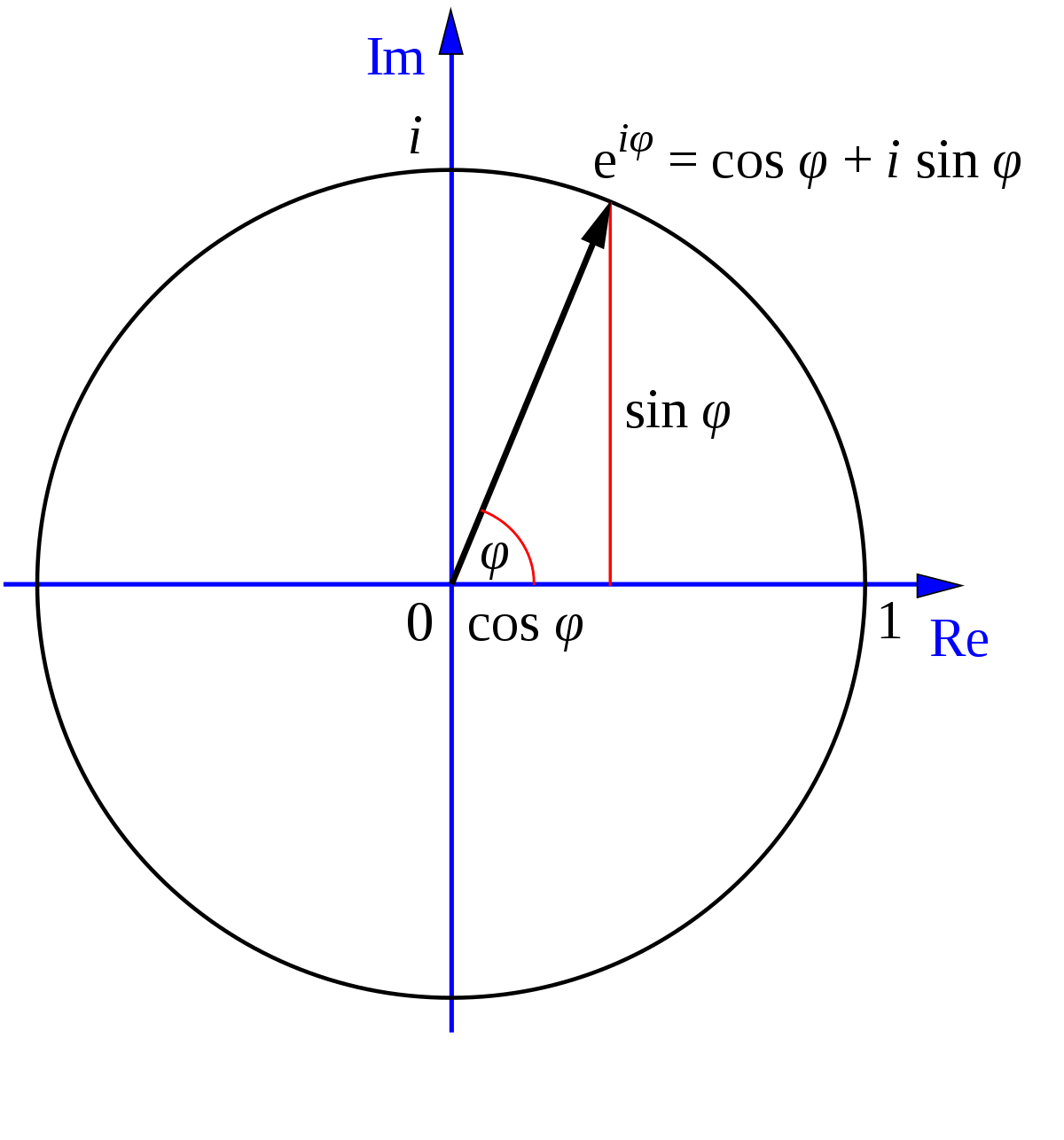
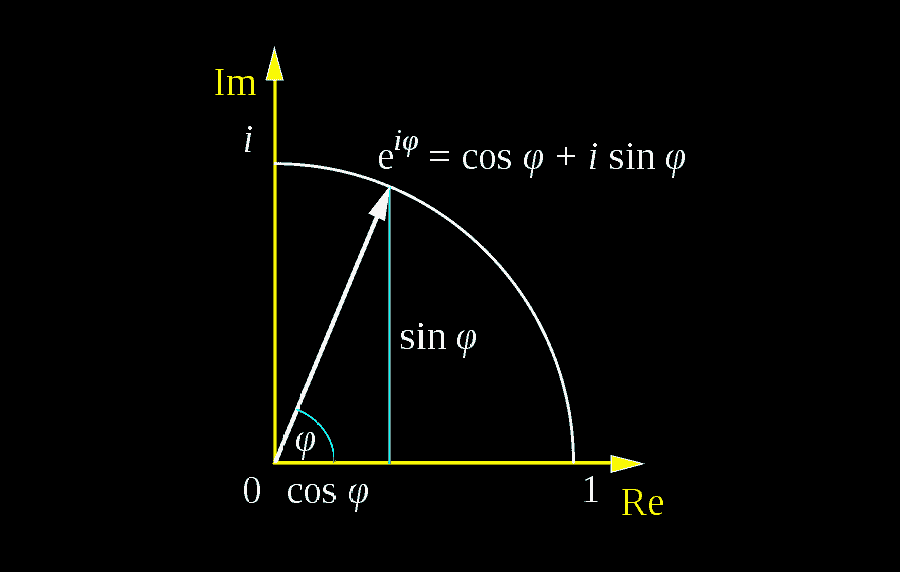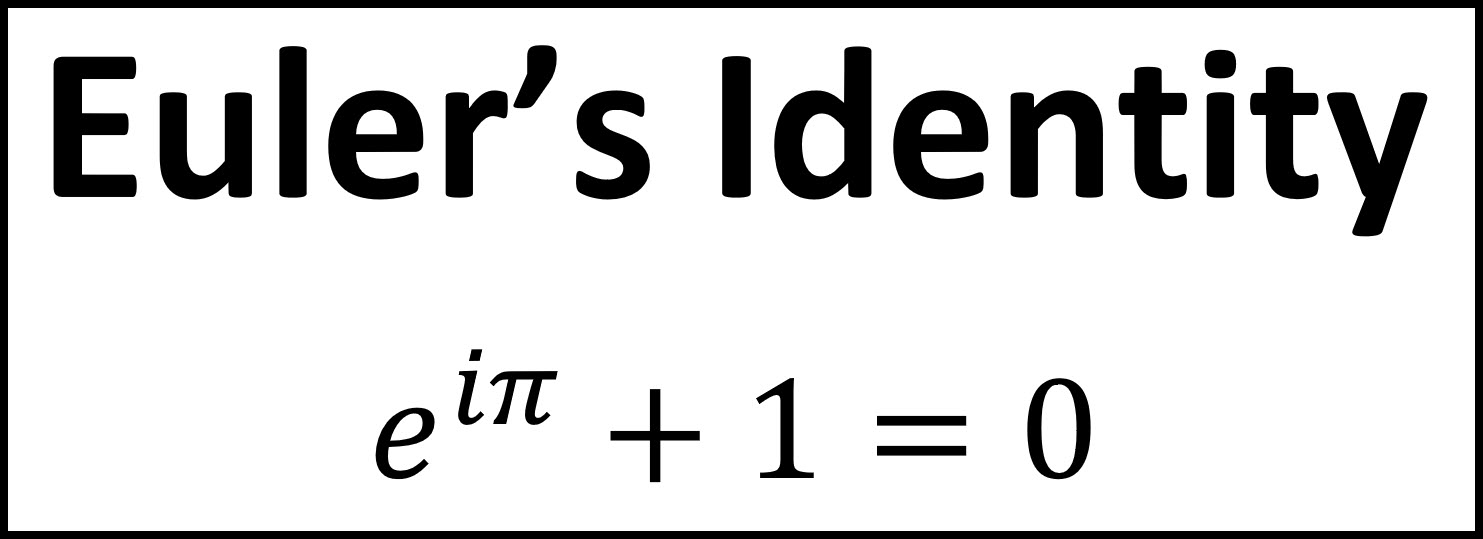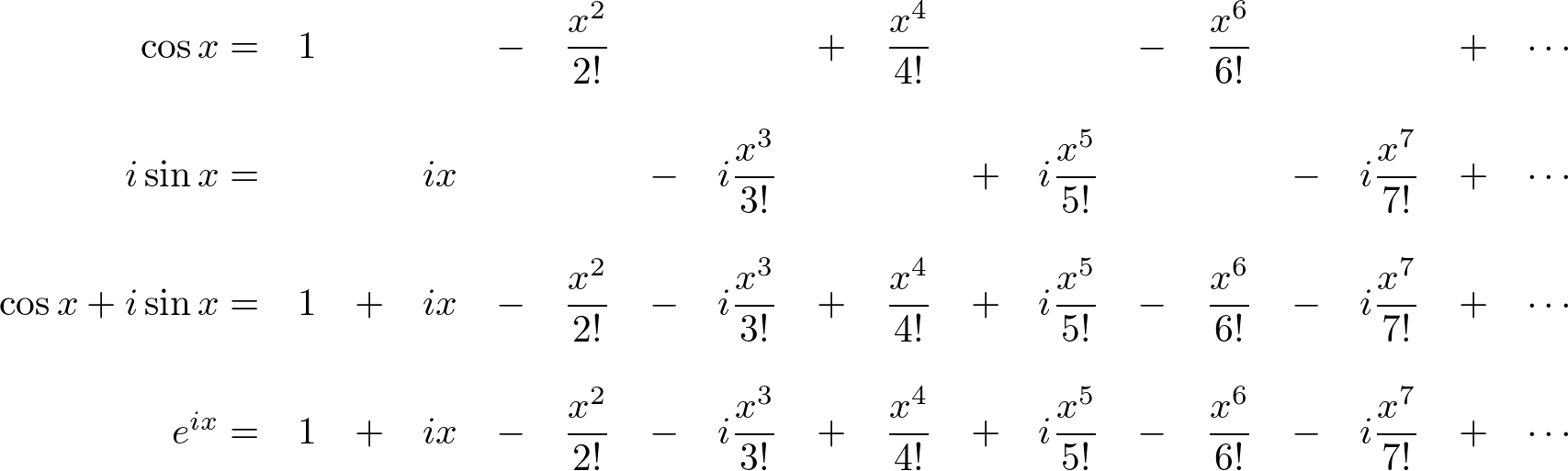Cosine In Euler Form
Cosine In Euler Form - The identities are useful in simplifying equations. Web sine and cosine are written as sums of complex exponentials. It is why electrical engineers need to. E i x = cos x + i sin x. Web euler's formula for product of cosines asked 7 years, 7 months ago modified 1 year, 10 months ago viewed 2k times 4 according to squaring the circle by ernest. Web v t e in mathematics, euler's identity [note 1] (also known as euler's equation) is the equality where e is euler's number, the base of natural logarithms, i is the imaginary unit, which. Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: That is, it defines a complex number that is one unit away. Using these formulas, we can. This formula is the most important tool in ac analysis.
Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. The number a + ib is represented by the. The complex plane complex numbers are represented geometrically by points in the plane: For example, if , then relationship to sin and cos in euler's. Using these formulas, we can. It turns messy trig identities into tidy rules for. Web sine and cosine are written as sums of complex exponentials. Suppose we have a function ∠\theta=\cos\theta+i\sin\theta; {\displaystyle e^{ix}=\cos x+i\sin x.} this formula is commonly considered for real values. Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions:
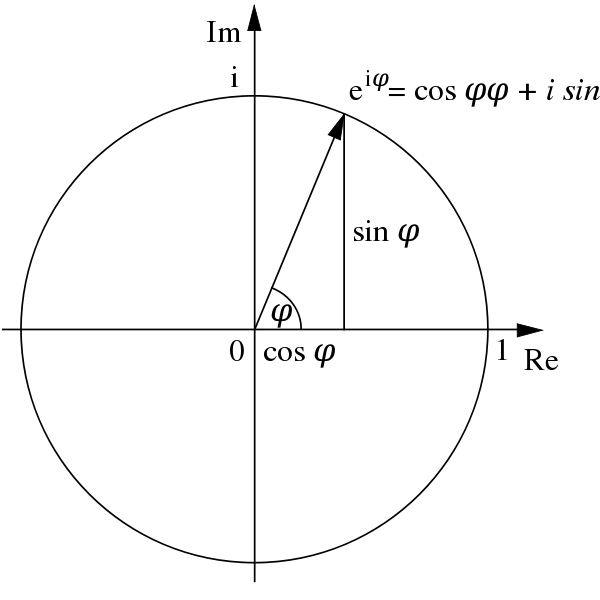
The complex plane complex numbers are represented geometrically by points in the plane: Web sine and cosine are written as sums of complex exponentials. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. E i x = cos x + i sin x. Let me try this from a different angle: Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. Using these formulas, we can. Web euler's formula for product of cosines asked 7 years, 7 months ago modified 1 year, 10 months ago viewed 2k times 4 according to squaring the circle by ernest. Web answer (1 of 9): It is why electrical engineers need to.
Direction Cosine Matrix Euler Integration Failure YouTube
The hyperbolic sine and the hyperbolic cosine. {\displaystyle e^{ix}=\cos x+i\sin x.} this formula is commonly considered for real values. Using these formulas, we can. The identities are useful in simplifying equations. Web euler's formula relates the complex exponential to the cosine and sine functions.
Trigonometric Form Into A Complex Number
Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: Let me try this from a different angle: Using these formulas, we can. Suppose we have a function ∠\theta=\cos\theta+i\sin\theta; The complex plane complex numbers are represented geometrically by points in the plane:
Euler's cosine wave YouTube
Web euler’s formula, polar representation 1. Web euler's formula relates the complex exponential to the cosine and sine functions. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. Web sine and cosine emerge from vector sum of three spinning numbers.
FileEuler's formula.svg New World Encyclopedia
{\displaystyle e^{ix}=\cos x+i\sin x.} this formula is commonly considered for real values. Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. E i x = cos x + i sin x. Web we can use euler’s theorem to.
Euler's Formula
Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. It turns messy trig identities into tidy rules for. Web euler's formula relates sine and cosine to the exponential.
Relationship between sine, cosine and exponential function
Web sine and cosine are written as sums of complex exponentials. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. Web euler's formula relates the complex exponential to the cosine and sine functions. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n.
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
E i x = cos x + i sin x. The number a + ib is represented by the. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:. Web euler's formula can be used to prove the addition.
Euler's Equation
Web euler's formula can be used to prove the addition formula for both sines and cosines as well as the double angle formula (for the addition formula, consider $\mathrm{e^{ix}}$. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. The hyperbolic sine and the hyperbolic cosine. Web euler's formula relates sine and cosine to the exponential.
Deriving the famous Euler’s formula through Taylor Series Muthukrishnan
The simple derivation uses euler's formula. The hyperbolic sine and the hyperbolic cosine. The complex plane complex numbers are represented geometrically by points in the plane: Web euler’s formula, polar representation 1. The identities are useful in simplifying equations.
Half Angles from Euler's Formula
Web v t e in mathematics, euler's identity [note 1] (also known as euler's equation) is the equality where e is euler's number, the base of natural logarithms, i is the imaginary unit, which. E i x = cos x + i sin x. That is, it defines a complex number that is one unit away. The identities.
Suppose We Have A Function ∠\Theta=\Cos\Theta+I\Sin\Theta;
Web euler's formula relates the complex exponential to the cosine and sine functions. Web sine and cosine emerge from vector sum of three spinning numbers in euler’s formula, the green spinning number is. For example, if , then relationship to sin and cos in euler's. Web finally, there is a nice formula discovered by leonhard euler in the 1700s that allows us to relate complex numbers, trigonometric functions and exponents into one single formula:.
Web We Can Use Euler’s Theorem To Express Sine And Cosine In Terms Of The Complex Exponential Function As S I N C O S 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒.
Web euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: Let me try this from a different angle: The identities are useful in simplifying equations. The hyperbolic sine and the hyperbolic cosine.
Web V T E In Mathematics, Euler's Identity [Note 1] (Also Known As Euler's Equation) Is The Equality Where E Is Euler's Number, The Base Of Natural Logarithms, I Is The Imaginary Unit, Which.
Web euler's formula relates sine and cosine to the exponential function: Web euler's formula for product of cosines asked 7 years, 7 months ago modified 1 year, 10 months ago viewed 2k times 4 according to squaring the circle by ernest. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. {\displaystyle e^{ix}=\cos x+i\sin x.} this formula is commonly considered for real values.
Web Sine And Cosine Are Written As Sums Of Complex Exponentials.
That is, it defines a complex number that is one unit away. This formula is the most important tool in ac analysis. The simple derivation uses euler's formula. Web euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines.