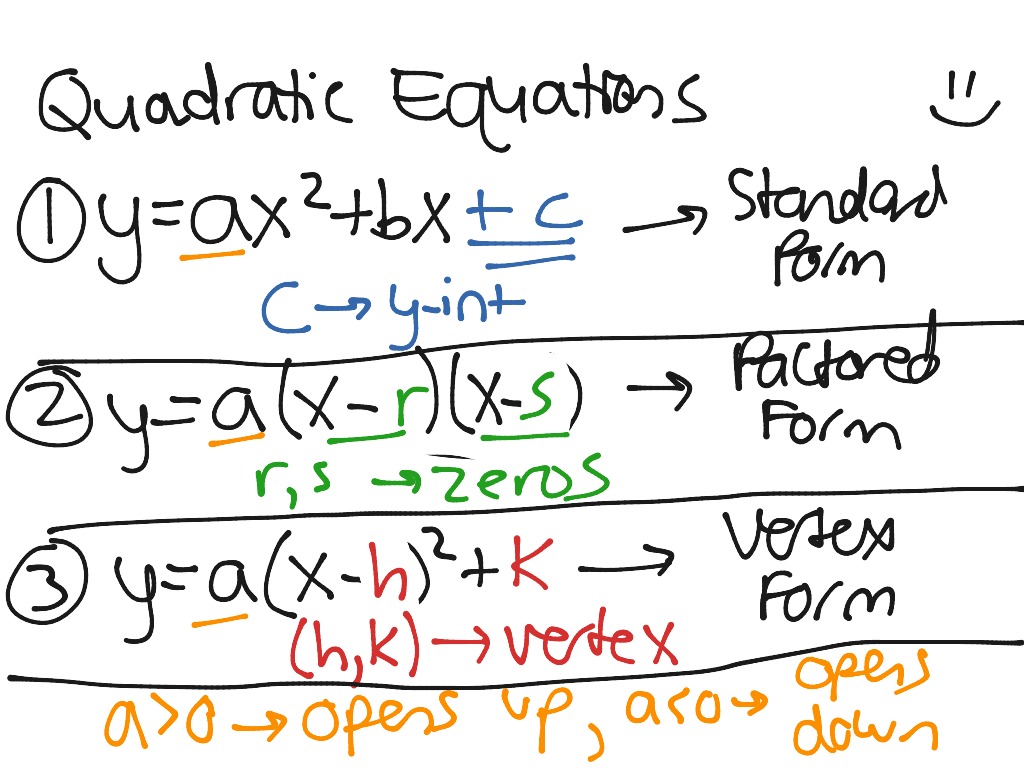Standard Form Vs Factored Form
Standard Form Vs Factored Form - Y = ax^2 + bx +c for some constants a,b,c vertex form: Y=ax^2+bx+c y = ax2 +bx+ c. Web assuming that we are talking about a quadratic equation in all cases: Web the stander ed form and the factored form both are related to the factor in mathematics. To see whether this works, for example, given the tetranomial. If no, move onto question 2. F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical stretch/shrink of the graph, and the direction the parabola is facing if |a| > 1 | a | > 1, the graph is vertically stretched Is there a common factor? If yes, factor out the gcf and continue to question 2. Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another.
Y=ax^2+bx+c y = ax2 +bx+ c. For the constant it is a, b, c. Y= ax 2 + bx + c = 0 is usually called the standard form. F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical stretch/shrink of the graph, and the direction the parabola is facing if |a| > 1 | a | > 1, the graph is vertically stretched Web 1 answer sorted by: Web so everyone agrees that standard form is generally a linear equation where you have some number times x plus some number times y is equal to some number. So things that are in standard form would include things like three x plus four y is equal to 10, or two x plus five y is equal to negative 10. Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another. Y = ( ax+b )( cx+d) or it can be as: There is no one true meaning to the phrase simplest form;
Web so everyone agrees that standard form is generally a linear equation where you have some number times x plus some number times y is equal to some number. Is there a common factor? Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another. Y = m(ax + b) ( cx + d) for related to some constant are: If no, move onto question 2. [why?] once this is the case, you can proceed to the following list of questions: For the constant it is a, b, c. Web 1 answer sorted by: A, b, c, d and m There is no one true meaning to the phrase simplest form;
Quadratic Eq factored form to general form Math, Algebra, Quadratic
To see whether this works, for example, given the tetranomial. 9.11k subscribers subscribe 4.9k views 2 years ago three forms of a quadratic. Y = ax^2 + bx +c for some constants a,b,c vertex form: You'll have to infer from context, or consult your textbook / professor to see if what they want is explicitly stated. For the constant it.
Converting Standard Form to Factored Form YouTube
[why?] once this is the case, you can proceed to the following list of questions: Y= ax 2 + bx + c = 0 is usually called the standard form. You'll have to infer from context, or consult your textbook / professor to see if what they want is explicitly stated. Web understanding standard form, factored form, and vertex form.
Relating Standard and Factored Form (Grade 11 mixed Lesson 3.1 22 3 13
Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another. 9.11k subscribers subscribe 4.9k views 2 years ago three forms of a quadratic. Web so everyone agrees that standard form is generally a linear equation where you have some number times x plus some number times y is equal to some.
2) Factored/Intercept Form
Y=ax^2+bx+c y = ax2 +bx+ c. Web 2 answers sorted by: A + b + c + d, a + b + c + d, F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical.
A1 Converting Standard Form to Factored Form YouTube
[why?] once this is the case, you can proceed to the following list of questions: Y = m(ax + b) ( cx + d) for related to some constant are: F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a.
Standard Form to Vertex Form? With Easy Examples Get Education Bee
Is there a common factor? [why?] once this is the case, you can proceed to the following list of questions: F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical stretch/shrink of the graph, and.
Polynomials Factored Form to Standard Form YouTube
Web 2 answers sorted by: A + b + c + d, a + b + c + d, So things that are in standard form would include things like three x plus four y is equal to 10, or two x plus five y is equal to negative 10. Y = ax^2 + bx +c for some constants a,b,c.
Standard form vs. factored form YouTube
Web so everyone agrees that standard form is generally a linear equation where you have some number times x plus some number times y is equal to some number. Y= ax 2 + bx + c = 0 is usually called the standard form. Web 1 answer sorted by: Web before starting any factoring problem, it is helpful to write.
ShowMe standard form
For the constant it is a, b, c. Y = ( ax+b )( cx+d) or it can be as: Web before starting any factoring problem, it is helpful to write your expression in standard form. Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another. F(x) = ax2 + bx +.
Changing Standard to Factored Form Grade 11 mixed Lesson 4 2 10 24 12
Web before starting any factoring problem, it is helpful to write your expression in standard form. For the constant it is a, b, c. F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical stretch/shrink.
Web The Stander Ed Form And The Factored Form Both Are Related To The Factor In Mathematics.
A, b, c, d and m 9.11k subscribers subscribe 4.9k views 2 years ago three forms of a quadratic. Web assuming that we are talking about a quadratic equation in all cases: Web 2 answers sorted by:
Web So Everyone Agrees That Standard Form Is Generally A Linear Equation Where You Have Some Number Times X Plus Some Number Times Y Is Equal To Some Number.
[why?] once this is the case, you can proceed to the following list of questions: For the constant it is a, b, c. Y=(ax+b)(cx+d) or possibly y=m(ax+b)(cx+d) for some constants a, b, c, d (and m) Each quadratic form looks unique, allowing for different problems to be more easily solved in one form than another.
If Yes, Factor Out The Gcf And Continue To Question 2.
Y=ax^2+bx+c y = ax2 +bx+ c. There is no one true meaning to the phrase simplest form; You'll have to infer from context, or consult your textbook / professor to see if what they want is explicitly stated. Web 1 answer sorted by:
Web Understanding Standard Form, Factored Form, And Vertex Form Of A Quadratic Equation Nabifroese Math Videos!
Y = ax^2 + bx +c for some constants a,b,c vertex form: A + b + c + d, a + b + c + d, F(x) = ax2 + bx + c f ( x) = a x 2 + b x + c can easily notice c c is the y y intercept a a tells you the vertical stretch/shrink of the graph, and the direction the parabola is facing if |a| > 1 | a | > 1, the graph is vertically stretched To see whether this works, for example, given the tetranomial.