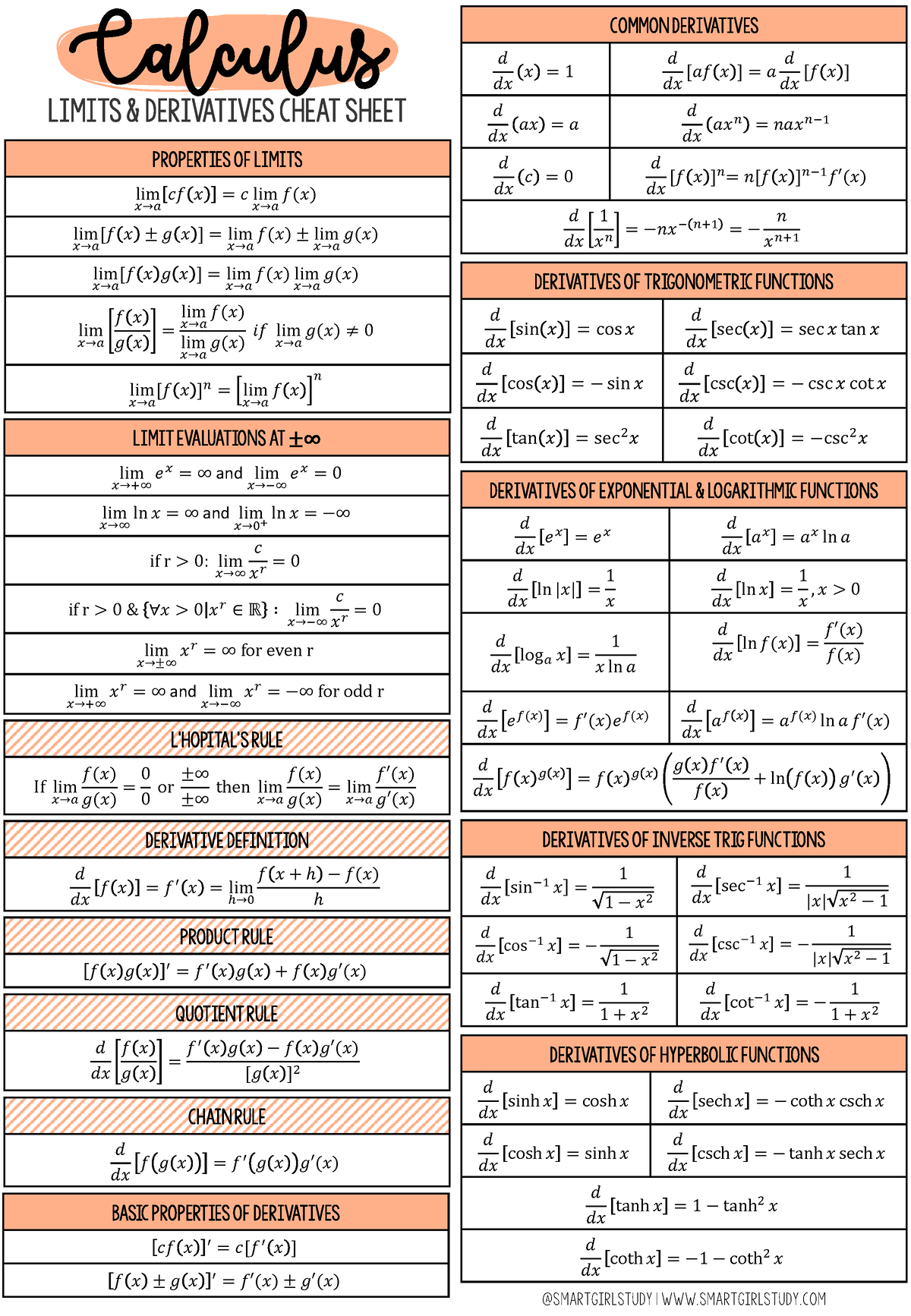
Limits Cheat Sheet

Limits Cheat Sheet - Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of a) without letting x = a. Same definition as the limit except it requires x. Where ds is dependent upon the form of the function being worked with as follows. 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Lim 𝑥→ = • squeeze theorem: Lim 𝑥→ = • basic limit: • limit of a constant: Let , and ℎ be functions such that for all ∈[ , ]. Ds = 1 dy ) 2.

Ds = 1 dy ) 2. Same definition as the limit except it requires x. Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of a) without letting x = a. Let , and ℎ be functions such that for all ∈[ , ]. 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Where ds is dependent upon the form of the function being worked with as follows. Lim 𝑥→ = • basic limit: Lim 𝑥→ = • squeeze theorem: • limit of a constant:

Lim 𝑥→ = • basic limit: Where ds is dependent upon the form of the function being worked with as follows. Ds = 1 dy ) 2. Let , and ℎ be functions such that for all ∈[ , ]. 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Lim 𝑥→ = • squeeze theorem: Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of a) without letting x = a. Same definition as the limit except it requires x. • limit of a constant:

Limits Worksheet With Answers Worksheet Now

2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Lim 𝑥→ = • basic limit: Let , and ℎ be functions such that for all ∈[ , ]. Same definition as the limit except it requires x. Ds = 1 dy ) 2.

Calculus Cheat Sheet i dont know la Limits & Derivatives Cheat

Let , and ℎ be functions such that for all ∈[ , ]. Lim 𝑥→ = • basic limit: • limit of a constant: 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Web we can make f(x) as close to l as we want by taking x sufficiently.

Limits Calculus Cheat Sheet Calculus Cheat Sheet

Same definition as the limit except it requires x. Lim 𝑥→ = • basic limit: Lim 𝑥→ = • squeeze theorem: 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Web we can make f(x) as close to l as we want by taking x sufficiently close to a.

Indeterminate forms of limits Math Worksheets & Math Videos Ottawa

Lim 𝑥→ = • basic limit: Where ds is dependent upon the form of the function being worked with as follows. Lim 𝑥→ = • squeeze theorem: Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of a) without letting x = a. Let , and ℎ.

SOLUTION Limits cheat sheet Studypool

• limit of a constant: Ds = 1 dy ) 2. Same definition as the limit except it requires x. Lim 𝑥→ = • squeeze theorem: Where ds is dependent upon the form of the function being worked with as follows.

Civil Law Time Limits Cheat Sheet Noah F. Schwinghamer, Esq

Same definition as the limit except it requires x. Lim 𝑥→ = • squeeze theorem: 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. • limit of a constant: Lim 𝑥→ = • basic limit:

Calculus Limits Cheat Sheet Calculus, Rational expressions, Precalculus

• limit of a constant: Lim 𝑥→ = • squeeze theorem: Let , and ℎ be functions such that for all ∈[ , ]. Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of a) without letting x = a. Ds = 1 dy ) 2.

Pin on Math cheat sheet

2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. • limit of a constant: Lim 𝑥→ = • squeeze theorem: Let , and ℎ be functions such that for all ∈[ , ]. Lim 𝑥→ = • basic limit:

Calculus Cheat Sheet All Limits Definitions Precise Definition We

Lim 𝑥→ = • basic limit: Same definition as the limit except it requires x. • limit of a constant: Where ds is dependent upon the form of the function being worked with as follows. Ds = 1 dy ) 2.

Calculus Limits Cheat Sheet

• limit of a constant: Lim 𝑥→ = • squeeze theorem: 2 dy y = f ( x ) , a £ x £ b ds = ( dx ) +. Ds = 1 dy ) 2. Web we can make f(x) as close to l as we want by taking x sufficiently close to a (on either side of.