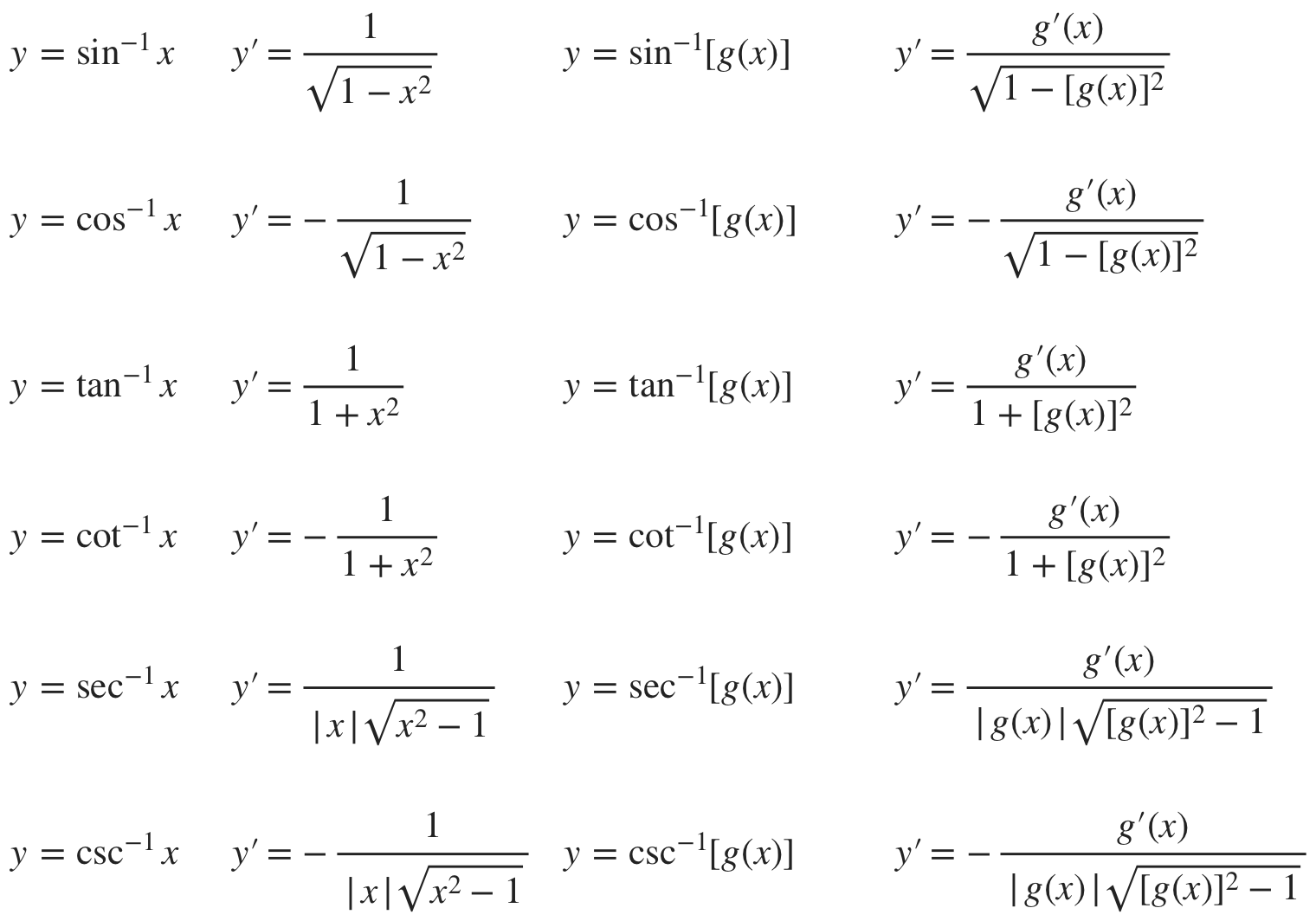Derivatives Of Trig Functions Cheat Sheet
Derivatives Of Trig Functions Cheat Sheet - Sum difference rule \left (f\pm. Web derivatives cheat sheet derivative rules 1. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Where c is a constant 2. (fg)0 = f0g +fg0 4. D dx (xn) = nxn 1 3. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. F g 0 = f0g 0fg g2 5. Web trigonometric derivatives and integrals: R strategy for evaluating sin:
(fg)0 = f0g +fg0 4. D dx (c) = 0; Web trigonometric derivatives and integrals: N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: R strategy for evaluating sin: F g 0 = f0g 0fg g2 5. Web derivatives cheat sheet derivative rules 1. Where c is a constant 2. D dx (xn) = nxn 1 3. Sum difference rule \left (f\pm.
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: (fg)0 = f0g +fg0 4. D dx (xn) = nxn 1 3. R strategy for evaluating sin: D dx (c) = 0; Sum difference rule \left (f\pm. Web derivatives cheat sheet derivative rules 1. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. F g 0 = f0g 0fg g2 5. Where c is a constant 2.
Derivatives of inverse trig functions Studying math, Physics and
Web trigonometric derivatives and integrals: F g 0 = f0g 0fg g2 5. R strategy for evaluating sin: N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Where c is a constant 2.
Finding inverse trig derivatives — Krista King Math Online math help
F g 0 = f0g 0fg g2 5. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. Sum difference rule \left (f\pm. R strategy for evaluating sin: Where c is a constant 2.
Integral Cheat Sheet Calculus derivative calc trig hyperbolic integral
F g 0 = f0g 0fg g2 5. D dx (xn) = nxn 1 3. Web trigonometric derivatives and integrals: Sum difference rule \left (f\pm. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin:
(PDF) Trig Cheat Sheet Jerome Delen Academia.edu
F g 0 = f0g 0fg g2 5. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: D dx (xn) = nxn 1 3. Sum difference rule \left (f\pm. D dx (c) = 0;
Trig cheat sheet linkjolo
(fg)0 = f0g +fg0 4. R strategy for evaluating sin: D dx (xn) = nxn 1 3. Web derivatives cheat sheet derivative rules 1. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos.
Trigonometry Laws and Identities Studying math, Math methods
D dx (c) = 0; F g 0 = f0g 0fg g2 5. (fg)0 = f0g +fg0 4. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: R strategy for evaluating sin:
Trig Cheat Sheet 1.4 PDF Trigonometric Functions Sine
Web derivatives cheat sheet derivative rules 1. F g 0 = f0g 0fg g2 5. Where c is a constant 2. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Web trigonometric derivatives and integrals:
Derivatives Cheat Sheet PDF
R strategy for evaluating sin: D dx (xn) = nxn 1 3. F g 0 = f0g 0fg g2 5. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. (fg)0 = f0g +fg0 4.
Pin on Math cheat sheet
(fg)0 = f0g +fg0 4. Sum difference rule \left (f\pm. Web derivatives cheat sheet derivative rules 1. F g 0 = f0g 0fg g2 5. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin:
Inverse Trig Derivatives (Derivatives of Inverse Trig Functions)
Where c is a constant 2. R strategy for evaluating sin: Web trigonometric derivatives and integrals: N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Sum difference rule \left (f\pm.
R Strategy For Evaluating Sin:
Where c is a constant 2. Web trigonometric derivatives and integrals: Sum difference rule \left (f\pm. Web derivatives cheat sheet derivative rules 1.
(Fg)0 = F0G +Fg0 4.
\tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. F g 0 = f0g 0fg g2 5. D dx (c) = 0; D dx (xn) = nxn 1 3.