2 2I In Polar Form

2 2I In Polar Form - Web get the free convert complex numbers to polar form widget for your website, blog, wordpress, blogger, or igoogle. Web the modulus or magnitude of a complex number ( denoted by ∣z∣ ), is the distance between the origin and that number. Approximate to two decimals if needed. Therefore, r = √22 + 22. A 2(cos 4π+isin 4π) b −2(cos 4π−isin 4π) c 2 2(cos 43π+isin 43π) d 2 2(cos 47π+isin 47π) e 2 2(cos 45π+isin 45π) hard solution. Write the complex number in polar form with argument θ in radians and between 0 and 2π. Answer verified 262.2k + views hint: By the above discussion, r = √a2 + b2 = | z |. Viewed 56 times 0 $\begingroup$. On complex numbers, see introductory lessons

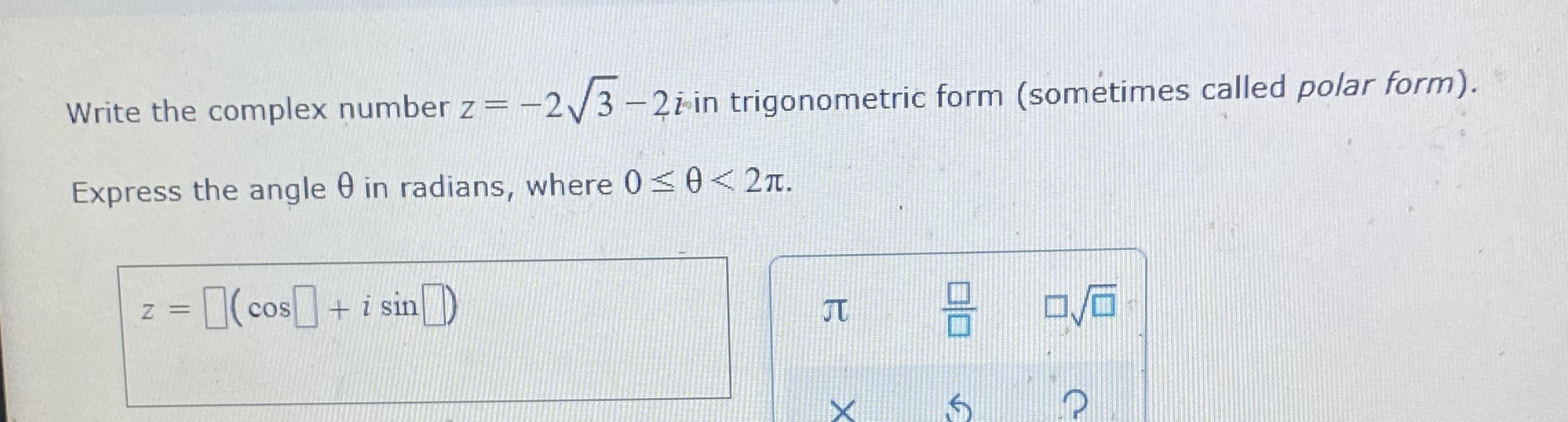
Write the complex number in polar form with argument θ in radians and between 0 and 2π. Web to write 2+2i into polar form we proceed as follows: Web let z = 2 + 2i be a complex number. In order to obtain the equivalent polar form of the given complex number, obtain. Web write the complex number −3 2+3 2i in the polar form. Web how do you write − 2 + 2 i in polar form? Web (1 + 3 i) = 2 (cos ⁡ 6 0 ∘ + i sin ⁡ 6 0 ∘) (1+\sqrt{3}i)=\goldd{2}(\cos\purplec{60^\circ}+i\sin\purplec{60^\circ}) (1 + 3 i) = 2 (cos 6. Approximate to two decimals if needed. R = √x2 +y2 r = x 2 + y 2 θ = tan−1 (y x) θ = t a. Viewed 56 times 0 $\begingroup$.

A) z=1+2i b) z=−4−21i c). Θ = tan−1( −2 2) = tan−1( −1) = − π 4 in 4th quadrant. ⇒ 2 − 2i = (2, −2) → (2√2, − π 4) answer link. Write the complex number in polar form with argument θ in radians and between 0 and 2π. Experts are tested by chegg as specialists in their subject area. Ask question asked 3 years, 6 months ago. Modified 3 years, 6 months ago. Approximate to two decimals if needed. By the above discussion, r = √a2 + b2 = | z |. Web get the free convert complex numbers to polar form widget for your website, blog, wordpress, blogger, or igoogle.

Write 2i in polar form. YouTube

Web how do you write − 2 + 2 i in polar form? Θ = tan−1( −2 2) = tan−1( −1) = − π 4 in 4th quadrant. In order to obtain the equivalent polar form of the given complex number, obtain. Web write the complete number −2−2i in polar form. R = √x2 +y2 r = x 2 +.

📈What is 2 + 2i in polar form?

Therefore, r = √22 + 22. Write the complex number in polar form with argument θ in radians and between 0 and 2π. A) z=1+2i b) z=−4−21i c). Ask question asked 3 years, 6 months ago. If the z = a +bi is a complex number than the.

Köp BeoPlay Form 2i

Approximate to two decimals if needed. Experts are tested by chegg as specialists in their subject area. By the above discussion, r = √a2 + b2 = | z |. Web write the complete number −2−2i in polar form. A 2(cos 4π+isin 4π) b −2(cos 4π−isin 4π) c 2 2(cos 43π+isin 43π) d 2 2(cos 47π+isin 47π) e 2 2(cos.

Solved 6) Write +2+ 2i in polar form (3 pt) HH

Θ = tan−1( −2 2) = tan−1( −1) = − π 4 in 4th quadrant. On complex numbers, see introductory lessons By the above discussion, r = √a2 + b2 = | z |. Viewed 56 times 0 $\begingroup$. 2+2i simplifying the above we get 2(1+i) dividing through above through by √2 =2*√2(1/√2+i/√2) but.

Complex Number 2 2i convert to Trigonometric Polar modulus argument

Write z in the polar form z = reiθ solution first, find r. If the z = a +bi is a complex number than the. Answer verified 262.2k + views hint: ⇒ r = √22 + ( −2)2 = √8 = 2√2. ⇒ 2 − 2i = (2, −2) → (2√2, − π 4) answer link.

express the complex number 2 2i into polar form Brainly.in

Web the modulus or magnitude of a complex number ( denoted by ∣z∣ ), is the distance between the origin and that number. A 2(cos 4π+isin 4π) b −2(cos 4π−isin 4π) c 2 2(cos 43π+isin 43π) d 2 2(cos 47π+isin 47π) e 2 2(cos 45π+isin 45π) hard solution. Θ = tan−1( −2 2) = tan−1( −1) = − π 4.

Solved Express 2 + 2i in polar form. Compute the value of

Web the modulus or magnitude of a complex number ( denoted by ∣z∣ ), is the distance between the origin and that number. Write z in the polar form z = reiθ solution first, find r. ⇒ r = √22 + ( −2)2 = √8 = 2√2. A) z=1+2i b) z=−4−21i c). Therefore, r = √22 + 22.

Answered Write the complex number z =2/3 2i in… bartleby

⇒ r = √22 + ( −2)2 = √8 = 2√2. Modified 3 years, 6 months ago. ⇒ 2 − 2i = (2, −2) → (2√2, − π 4) answer link. By the above discussion, r = √a2 + b2 = | z |. Web how do you write − 2 + 2 i in polar form?

i. Write z = 2i in polar form.. ii. find the Gauthmath

Web write the complete number −2−2i in polar form. Answer verified 262.2k + views hint: Web the first step toward working with a complex number in polar form is to find the absolute value. 2+2i simplifying the above we get 2(1+i) dividing through above through by √2 =2*√2(1/√2+i/√2) but. R = √x2 +y2 r = x 2 + y 2.

Misc 5 Convert in polar form (i) (1 + 7i)/(2 i)2 Miscellaneous

Web (1 + 3 i) = 2 (cos ⁡ 6 0 ∘ + i sin ⁡ 6 0 ∘) (1+\sqrt{3}i)=\goldd{2}(\cos\purplec{60^\circ}+i\sin\purplec{60^\circ}) (1 + 3 i) = 2 (cos 6. Find more mathematics widgets in wolfram|alpha. Web how do you write − 2 + 2 i in polar form? A 2(cos 4π+isin 4π) b −2(cos 4π−isin 4π) c 2 2(cos 43π+isin 43π).

A 2(Cos 4Π+Isin 4Π) B −2(Cos 4Π−Isin 4Π) C 2 2(Cos 43Π+Isin 43Π) D 2 2(Cos 47Π+Isin 47Π) E 2 2(Cos 45Π+Isin 45Π) Hard Solution.

⇒ r = √22 + ( −2)2 = √8 = 2√2. Therefore, r = √22 + 22. On complex numbers, see introductory lessons Find more mathematics widgets in wolfram|alpha.

The Absolute Value Of A Complex Number Is The Same As Its Magnitude, Or | Z |.

Viewed 56 times 0 $\begingroup$. Web write the complete number −2−2i in polar form. Web let z = 2 + 2i be a complex number. If the z = a +bi is a complex number than the.

⇒ 2 − 2I = (2, −2) → (2√2, − Π 4) Answer Link.

Answer verified 262.2k + views hint: Web the first step toward working with a complex number in polar form is to find the absolute value. 2+2i simplifying the above we get 2(1+i) dividing through above through by √2 =2*√2(1/√2+i/√2) but. Modified 3 years, 6 months ago.

Ask Question Asked 3 Years, 6 Months Ago.

Write the complex number in polar form with argument θ in radians and between 0 and 2π. Write z in the polar form z = reiθ solution first, find r. Web how do you write − 2 + 2 i in polar form? Web the modulus or magnitude of a complex number ( denoted by ∣z∣ ), is the distance between the origin and that number.